非平衡熱力学の知見から拡散モデルの最適手法を提案 ―熱力学的散逸と生成誤差をつなぐ関係式を導出―
発表のポイント
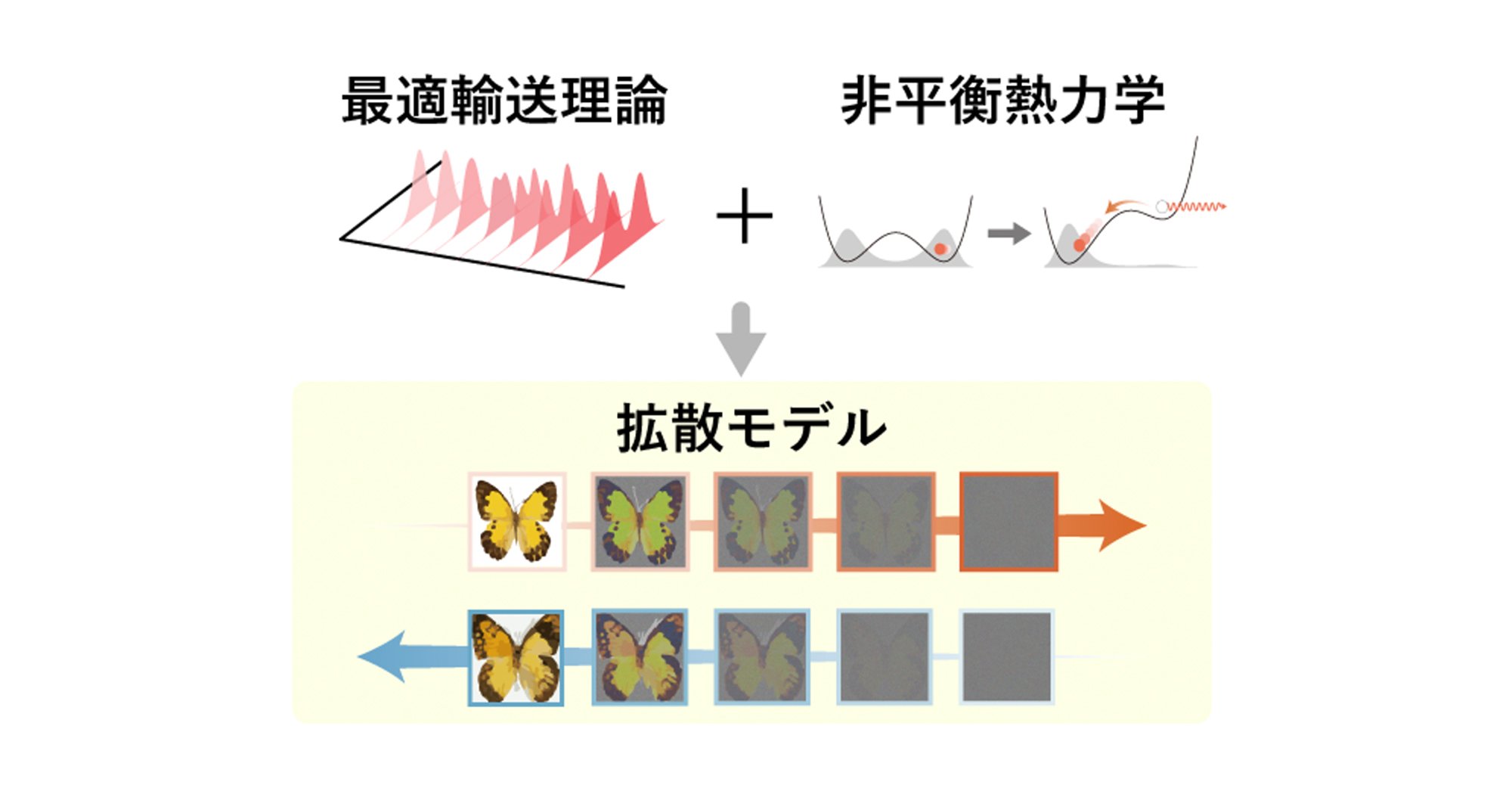
◆ 非平衡熱力学におけるトレードオフ関係式のアナロジーを拡散モデルに応用することで、拡散モデルを用いた時の生成誤差と拡散における散逸の量との間の関係式を導出しました。◆ 拡散モデルの訓練で重要となるノイズスケジュールについて、最適輸送と呼ばれるスケジュールを用いると生成精度を最も上昇させうることを理論的に示しました。◆ 本研究は非平衡熱力学が生成モデルの手法において有用であることを示したものであり、今後非平衡熱力学の知見に基づく生成モデルの研究が発展していくことが期待できます。
非平衡熱力学と最適輸送理論を用いて拡散モデルを解析
概要
東京大学工学部計数工学科の池田滉太郎学部4年生、東京大学理学部地球惑星物理学科の宇田智哉学部4年生、株式会社 Preferred Networksの岡野原大輔代表取締役 CTO、東京大学大学院理学系研究科の伊藤創祐准教授は、非平衡熱力学(注1)における熱力学的なトレードオフ関係(注2)のアナロジーによって、非平衡熱力学を用いて拡散モデル(注3)によって生成したデータの生成精度を評価できることを明らかにしました。本研究では拡散モデルにおいて、生成誤差と熱力学的な散逸の量(注4)を結びつける熱力学的な不等式を導出しました。特にこの不等式を用いて、今まで拡散モデルの訓練時に経験的に決められてきたノイズスケジュール(注5)の選択において、最適輸送理論(注6)に基づいたノイズスケジュールを用いることが生成誤差の最小化に寄与することを理論的に示しました。この研究はこれまで理論的な根拠が薄いまま行われてきたノイズスケジュールの選択に、非平衡熱力学という視点から理論的な根拠を与えることになりました。また今後は本研究に基づいて、非平衡熱力学的な視点が拡散モデルなどの生成モデルの手法の改善・提案に貢献する可能性を与えます。本研究の一部は東京大学生物普遍性連携研究機構が同大学前期教養学部で開講している全学自由研究ゼミナール「生命の普遍原理に迫る研究体験ゼミ」の一環として行われました。本研究成果はPhysical Review X誌に掲載されました。発表内容
拡散モデルは生成AIに用いられる生成モデル技術の一つであり、高品質な画像や動画を生成する応用によって注目を集めています。この拡散モデルは入力データにノイズを加えていく順過程と、順過程から学習したダイナミクスの情報を用いて、時間を逆向きに遡るようにノイズからデータを生成する逆過程から構成されています(図1)。入力データにノイズを加えていく順過程は拡散過程の一種とみなすことができます。拡散過程において順過程と逆過程を比較して不可逆性を議論することは非平衡熱力学の分野で以前から行われており、実際この拡散モデルは非平衡熱力学におけるそのような研究の視点から着想された手法です。このように拡散モデルは非平衡熱力学による着想から端を発するにも関わらず、これまでの先行研究では拡散モデルの解析において非平衡熱力学の知見はほとんど利用されてきませんでした。
図1:拡散モデルの概要図拡散モデルは訓練データにノイズを加える順過程と順過程で学習した情報をもとにデータを生成する逆過程から構成されています。順過程における拡散後のデータと逆過程において新しく生成されたノイズは一般には異なり、その影響で訓練データと生成データの差、つまり、生成誤差が生じます。
特に注目に値する非平衡熱力学の知見の一つに、熱力学的なトレードオフ関係があります。例えばその一種である速度限界と呼ばれる不等式は、最適輸送理論と深い関わりがあり、有限時間での非準静的な操作において熱力学的な散逸が最も少なくなるような状況は最適輸送と結びついていることを主張しています。さらに最適輸送理論の知見は拡散モデルを含む様々な生成モデルの手法において広く使われています。このように非平衡熱力学の考え方と拡散モデルに代表される生成モデルの手法の間には、最適輸送理論の手法に代表されるような関係性が見出せるものの、生成モデルの研究においてこれまで非平衡熱力学の知見が適切に使われることはありませんでした。そこで研究グループは、熱力学的なトレードオフ関係のアナロジーを用いることで、拡散モデルにおいても新たに生成誤差と熱力学的な散逸に関する関係式を導出しました。
実際、拡散モデルにおいて順過程の終端で得られるデータと逆過程の最初に新しく生成したノイズは一般に異なります(図1)。拡散モデルにおける順過程のダイナミクスの情報の学習が仮に正確に行えていたとしても、このノイズ同士の差によって訓練データと出力データの差、すなわち生成誤差が原理上発生してしまいます。今回は逆過程の初期時点におけるノイズのずれに起因した、ずれの大きさで適切に規格化した生成誤差の増加量に注目しました(図2)。生成誤差の増加量が小さい拡散モデルは、初期ノイズのずれに対して生成誤差が大きく発生しないため、安定した生成ができるモデルであると言えます。この意味で、生成誤差の増加量が小さい拡散モデルは生成精度の「良い」モデルであると言えます。
図2:今回導いた関係式の概念図
今回導いた関係式は非平衡熱力学における熱力学的な散逸と拡散モデルにおける生成誤差の増加量を結びつけるものです。具体的には、今回の関係式は、生成誤差の増加量は順過程における熱力学的な散逸で表される量で上から抑えられることを主張しています。
今回導いた関係式は適切に定義された生成誤差の増加量の指標が熱力学的な散逸の指標よりも常に小さくなることを示すものです(図2)。この熱力学的な散逸の指標は順過程のダイナミクスをどう構成するかによって値が変わります。この関係式によると、順過程のダイナミクスとして熱力学的な散逸の指標を最も小さくできるものを選択することで、生成誤差の増加量がより小さい安定したデータ生成の実現が可能となります。またこの順過程のダイナミクスとして熱力学的な散逸の指標を最も小さくできるのは、最適輸送と呼ばれるダイナミクスであることがこれまで非平衡熱力学の分野で見出されてきました。よって、非平衡熱力学の知見と今回導いた関係式に基づくと、最適輸送に基づく順過程が生成誤差の増加量を最も小さく保つことができるということがわかります。実際、このような順過程のダイナミクスの選択は拡散モデルにおいては重要な問題であり、ノイズスケジュールの選択という観点から数多くの議論がなされてきました。これまで経験的にうまくいくとされているノイズスケジュールは、拡散モデルにおいて様々な形で提案されており、とりわけ最適輸送に基づくスケジュールが生成誤差を小さくするのに効果的であることが知られていました。本研究は、これまで経験的に有効とされてきた「最適輸送に基づくノイズスケジュール」が最適であることを、今回導いた関係式によって非平衡熱力学の視点から理論的に示したと評価できます。さらに、得られた関係式が具体的な拡散モデルによるデータ生成において、適切に機能していることも数値的に検証しました。今回の研究により、非平衡熱力学の視点によって拡散モデルという生成モデルの手法における最適性を示すことが可能になりました。生成モデルにおける非平衡熱力学の有用性を示すことに成功したため、今後も拡散モデルを含む生成モデルや機械学習の手法に対して、非平衡熱力学に基づいて理論的な根拠を探究していくという新たな方向性の研究が発展していくことが見込まれます。さらに、同様の非平衡熱力学に基づいたアイディアによって、生成モデルの改善手法の発見や、機械学習における新手法の提案につながっていくかもしれません。
発表者情報
東京大学
工学部 計数工学科
池田 滉太郎 学部4年生
理学部地球惑星物理学科
宇田 智哉 学部4年生
大学院理学系研究科 附属生物普遍性研究機構・物理学専攻
伊藤 創祐 准教授
株式会社 Preferred Networks
岡野原 大輔 代表取締役 最高技術責任者
論文情報
雑誌名:Physical Review X
題 名:Speed-accuracy relations for diffusion models: Wisdom from nonequilibrium thermodynamics and optimal transport
著者名:Kotaro Ikeda, Tomoya Uda, Daisuke Okanohara, and Sosuke Ito*
DOI: 10.1103/x5vj-8jq9
URL: https://doi.org/10.1103/x5vj-8jq9
研究助成
本研究は、科研費「微分幾何学に基づいた非平衡熱力学における普遍的原理の探究(課題番号:22H01141)」、「ゆらぎの熱力学に基づく確率的コンピューティング基盤の創出(課題番号:23H00467)」、「幾何学的な最適性に基づく熱力学的なトレードオフ関係の量子拡張(課題番号:24H00834)」、「金融市場ミクロデータ解析によるHFTの実態調査と流動性シミュレーターの構築(課題番号:21H01560)」、科学技術振興機構 ERATO「情報エネルギー変換 (課題番号: JPMJER2302)」、UTEC-UTokyo FSI Research Grant Programの支援により実施されました。
用語解説
(注1)非平衡熱力学
時間変化するダイナミクスに基づいて、不可逆な流れが発生している系での状態変化や、熱力学的な散逸について研究する統計物理学の一分野です。近年、ゆらぎの熱力学と呼ばれる拡散現象における非平衡熱力学において、情報理論における様々な指標との関わりが注目されています。
(注2)熱力学的なトレードオフ関係
熱力学的な散逸に関する量と、状態変化の速度や状態の揺らぎの大きさ、正確性など様々な系のパフォーマンスに関する量との間を不等式によって結びつける関係式の総称です。熱力学的なトレードオフ関係の一種として、最適輸送理論に基づいて有限時間の状態変化で発生する熱力学的な散逸と、状態間の変化のスピードを結びつける速度限界があります。
(注3)拡散モデル
データにノイズを加える拡散過程を学習して、時間逆向きの時間発展を再現することで、訓練データセットに含まれていないような新しいデータを生成する機械学習モデル(生成モデル)の一種です。近年では画像や動画の生成AIに利用され、高品質なデータ生成が可能である点で注目を集めています。この手法は時間順方向のダイナミクスと時間逆方向のダイナミクスの統計的な差から熱力学的な散逸を議論する非平衡熱力学の考え方にインスパイアされて着想されました。
(注4)熱力学的な散逸の量
非平衡熱力学において、状態間変化における不可逆性を記述する量であり、代表的な量としてエントロピー生成率と呼ばれるものがあります。このエントロピー生成率は常に非負であり、その非負性は熱力学第二法則と呼ばれる熱力学における重要な法則として知られています。本研究で得られた関係式では、このエントロピー生成率に温度をかけて時間積分した量を用いています。
(注5)ノイズスケジュール
拡散モデルにおける順過程においては、ノイズの強度をどのように時間変化させて加えていくか、というのが順過程のダイナミクスの仕方を決めます。そのためこのような順過程のダイナミクスの決め方は、一般にノイズスケジュールと呼ばれています。このノイズスケジュールの違いによって生成精度が異なることがこれまでよく知られており、どのようなノイズスケジュールを使うべきかについて様々な議論がこれまで行われてきました。
(注6)最適輸送理論
輸送コストを最小化するにはどのような輸送をすれば良いのか、という問題から始まった数学の分野です。これまで輸送コストの最小化の視点から、確率分布間の距離(Wasserstein距離)の指標が作られたり、輸送コストを最小化する確率分布の時間的な変化のさせ方が提案されたりしてきました。これまで機械学習の分野では、データ間の違いを最適輸送理論から定義される距離を用いることで、その違いを評価してデータの生成などを行ってきました。また輸送コストを最小化する確率分布の時間的な変化のさせ方の考え方も拡散モデルにおいて取りいれられてきました。一方で非平衡熱力学の分野でも、非平衡熱力学と最適輸送理論の密接な関係が近年急速に理解されており、最適輸送による確率分布の時間変化により最小の散逸が達成されることがわかっています。
プレスリリース本文:PDFファイル
Physical Review X:https://doi.org/10.1103/x5vj-8jq9



