ゴムの鋭い亀裂は粘弾性から生じる～ノーベル賞受賞者30年来の理論を証明～

ポイント

ゴムが一瞬で壊れる「高速破壊」時に、なぜ亀裂先端が鋭くとがるのかは長年未解明だった。
ノーベル物理学賞受賞者ド・ジェンヌ博士が提唱した「粘弾性トランペット理論」を連続体力学の基礎方程式から初めて導き、ゴムの基本的性質である粘弾性だけで鋭化が生じることを数学的に証明した。
タイヤから医療材料まで、幅広いポリマー材料の破壊制御や耐久性向上の理論的基盤となることが期待される。

JST 戦略的創造研究推進事業において、大阪大学大学院基礎工学研究科の長滝谷北斗大学院生（博士後期課程）、小林舜典助教、垂水竜一教授とZEN大学知能情報社会学部作道直幸准教授（兼：東京大学大学院工学系研究科特任准教授）の研究グループは、ゴムの高速破壊の際に亀裂先端が鋭くとがるメカニズムを、世界で初めて数学的に解明しました。

ゴム風船が割れたり、タイヤが破裂（バースト）したりするのは、微小な亀裂が一瞬で広がる「高速破壊」によるものです。このとき、亀裂先端が鋭化し破壊が加速しますが、なぜ鋭化するのかは長年解明されておらず、従来は材料の複雑な非線形効果^注1）が原因と考えられてきました。

本研究グループは、亀裂進展の問題を数学的に厳密に解き、亀裂の形状と材料全体の変形を記述する数式を導出しました。これにより、亀裂先端の鋭化が、ゴムなどのポリマー材料（高分子材料）^注2）が持つ基本的な性質である「粘弾性^注3）」だけで生じることを証明しました。さらに、ノーベル物理学賞受賞者ド・ジェンヌ博士^注4）が約30年前に提唱した「粘弾性トランペット理論^注5^）」を、連続体力学^注6）の基礎方程式から数学的に証明しました。

本成果は、タイヤから医療材料まで幅広い粘弾性材料の破壊制御の理論的基盤となり、製品の耐久性向上や事故防止、長寿命化による環境負荷低減への貢献が期待されます。

本成果は、2025年10月1日（現地時間）に米国の学術誌「Physical Review Research」にLetterとしてオンラインで公開されました。

本成果は、以下の支援によって得られました。

戦略的創造研究推進事業総括実施型研究（ERATO）

研究領域：「酒井複素ゲルプロジェクト」（課題番号：JPMJER2401）

研究総括：酒井崇匡（東京大学大学院工学系研究科教授）

研究期間：2024年10月～2030年3月

上記研究領域では、ゲルの構造や性質とその法則を解き明かすことで、ゲルを設計可能な素材へと進化させ、新たな価値創造へつなげることを目的としています。

戦略的創造研究推進事業個人型研究（さきがけ）

研究課題：「材料多様体のマルチスケールメカニクス」（課題番号：JPMJPR1997）

研究代表者：垂水竜一（大阪大学大学院基礎工学研究科教授）

創発的研究支援事業（FOREST）

研究課題：「高分子ゲルの普遍的熱力学・動力学・破壊力学の構築」（課題番号：JPMJFR232A）

研究代表者：作道直幸（ZEN大学知能情報社会学部准教授、東京大学大学院工学系研究科特任准教授）

そのほか、日本学術振興会（JSPS）科学研究費補助金基盤研究（B）「ゲル弾性論の構築：負のエネルギー弾性とネットワークトポロジーの寄与の解明（研究代表者：作道直幸、課題番号：JP23K22458・JP22H01187）」、「精密ゲル科学に基づくゲル弾性論と浸透圧原理の解明（研究代表者：作道直幸、課題番号：JP25K00966）」による支援を受けて行われました｡

＜研究の背景と経緯＞

私たちの身の回りには、ゴムやゲルのような柔らかく伸び縮みする「ポリマー材料」で作られた製品があふれています。輪ゴムや風船、自動車のタイヤ、医療用カテーテルなど、その用途は多岐にわたります。これらの材料は非常に便利ですが、輪ゴムがパチンと切れる、膨らんだ風船が破裂する、タイヤがバーストするなど、予告なく一瞬で壊れることがあります。こうした突然の破壊は、材料の中に生じた微小な亀裂が、一瞬のうちに材料全体へと広がることで引き起こされます。

このような突然の破壊を避けるための研究において「亀裂先端の鋭化」が注目されています。亀裂の進展速度が遅いとき、亀裂先端は丸みを帯びた放物線形状です。しかし、亀裂が高速で進展すると先端が鋭くとがります。この鋭化が破壊をさらに加速させ、材料の突然の破壊につながると考えられています。

しかし、「なぜ亀裂の進展が高速になると鋭くとがるのか？」という根本的な問いへの答えは謎のままでした。線形弾性破壊力学と呼ばれる標準的な理論では、亀裂先端は常に放物線形状と予測され、鋭化現象を説明できません。そのため、材料が大きく引き伸ばされた際の複雑な非線形効果が原因というのが定説ですが、この仮説だけでは全ての実験結果を説明できません。メカニズムが不明なため、より安全で耐久性の高い材料の開発は、試行錯誤に頼らざるを得ない状況でした。

＜研究の内容＞

今回、本研究グループは、粘弾性固体における亀裂進展の問題を世界で初めて数学的に解き、「亀裂先端の鋭化」の謎を解明しました。従来、動的な破壊の問題は極めて複雑で、限られたパラメーター範囲しか扱えないコンピューターシミュレーションに頼る研究がほとんどでした。しかし本研究では、動的な亀裂進展を静止した亀裂の問題に変換し、変換された問題を解いてから元の動的な亀裂進展の問題に戻す新しい数学的手法^注7）を開発し、亀裂の形状と材料内部のひずみ分布を表す数式の導出に成功しました。

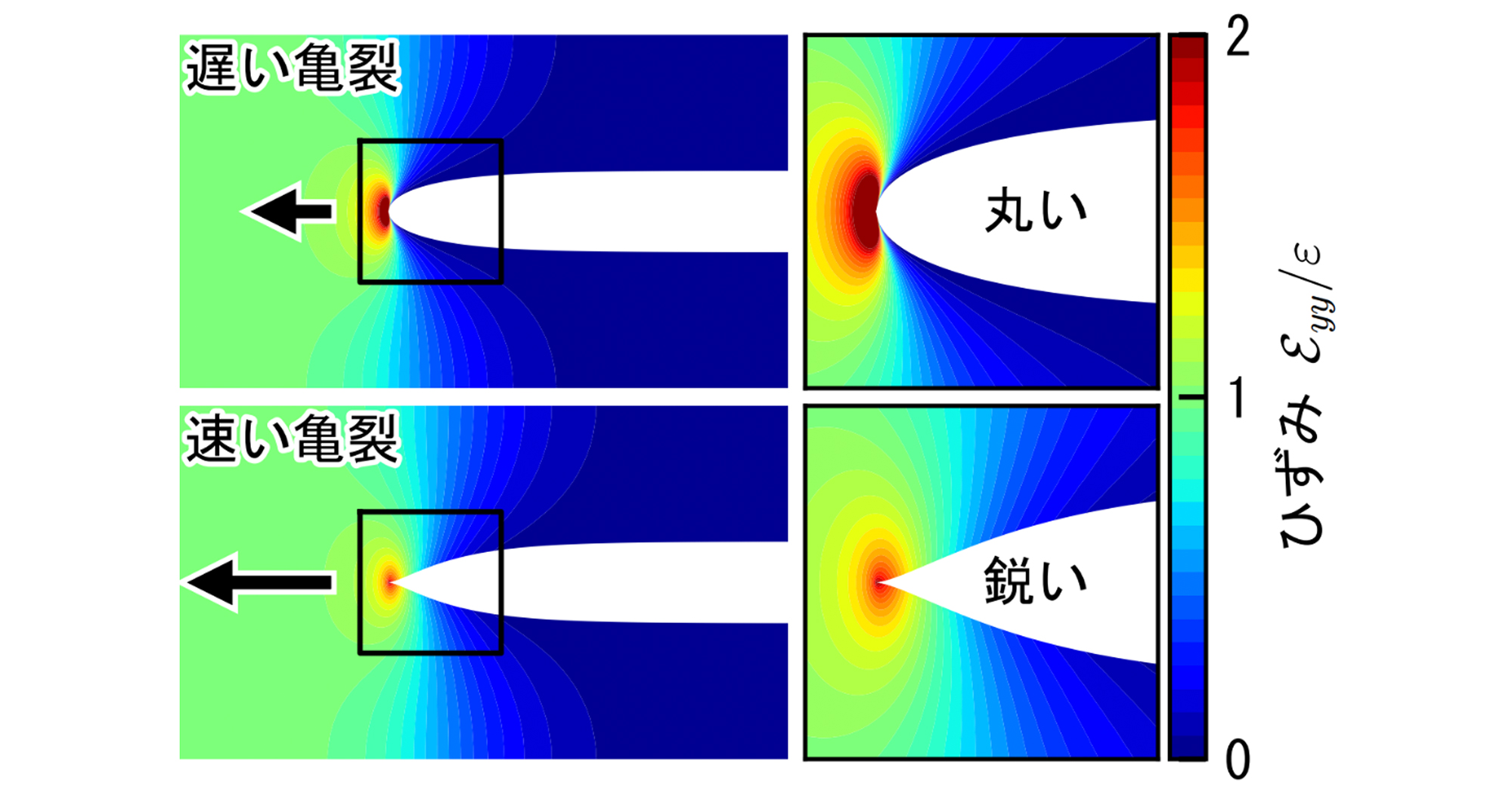
導出された数式から、亀裂先端の鋭化がゴムの基本的性質である「粘弾性」だけで説明できることが分かりました。粘弾性とは、引っ張る速さによって材料の状態が変わる性質です。ゆっくり引っ張ると柔らかい「ゴム状態」、速く引っ張ると発熱する「粘性状態」、さらに速く引っ張ると硬い「ガラス状態」になります。高速で進展する亀裂では、先端付近がガラス状態、中間が粘性状態、遠方がゴム状態となります。亀裂進展が速くなると、粘性状態の領域が広がることで先端が鋭くとがります（図1）。これは「複雑な非線形効果が必要」という従来の定説を覆す発見です。

本研究により、3つの領域の境界と各領域での亀裂形状を決める「べき乗則^注8）」の指数がすべて明らかになりました（図2）。驚くべきことに、導出された指数は、ノーベル物理学賞受賞者のド・ジェンヌ博士が約30年前に提唱した「粘弾性トランペット理論」と完全に一致しました。ド・ジェンヌ博士はスケーリング理論により亀裂がトランペットのような形状になると予想しましたが、導出は数学的に厳密ではなく、通常の破壊力学との関係は不明でした。当初、本研究は、粘弾性トランペット理論を反証できると予想して始めましたが、結果的に、理論が連続体力学の基礎方程式から厳密に導かれることを示し、30年来の理論に決定的な数学的根拠を与えました。

さらに、ド・ジェンヌの理論では扱われていなかった材料全体のひずみ分布も明らかにし、最近の実験で観測された亀裂前方における「ひずみが一定になるプラトー領域」が粘弾性により生じることを解明しました。

本成果は、数値計算でしか扱えなかった複雑な動的破壊問題に厳密な数学的解を与え、物理的直感に基づいていたド・ジェンヌの理論を、連続体力学の基礎方程式から証明した点で画期的です。

図1　亀裂の進展速度による亀裂先端形状の変化とひずみ分布

（上図）亀裂の進展速度が遅いときは亀裂先端が丸い放物線形状を示す。（下図）亀裂の進展速度が速くなると、粘弾性効果により亀裂先端が鋭くとがる。ゴムやゲルの破壊実験では、縦幅が数センチメートルから数十センチメートルのサンプルを用いることが多い。なお、亀裂先端のとがり具合は、材料の粘弾性緩和時間（ゴム状態から粘性支配の状態に移り変わる時間スケール）と亀裂進展速度の積から決まる（図2参照）。

図2　数学的な解が明らかにした亀裂面の形状

亀裂先端からの距離に応じて、亀裂面の変位がべき乗則（1/2乗、3/2乗、1/2乗）に従う3つの領域（ガラス領域、粘性領域、ゴム領域）に分かれ、全体としてトランペットのような形状を示す。このグラフは、両方の軸が対数目盛になっている「両対数グラフ」として書かれている。両対数グラフでは、1目盛りが10倍、2目盛りが100倍、3目盛りが1000倍に対応し、べき乗則の指数がグラフの傾きで表される。「粘性領域とゴム領域の境界」の位置x_c は、材料の粘弾性緩和時間と亀裂進展速度の積で決まり、先端のとがりの長さを与える。x_c が短ければ先端が放物線状に見える。

＜今後の展開＞

本研究の成果は、破壊における粘弾性の役割を明らかにしたことで、粘弾性を持つポリマー材料の破壊現象の理解を大きく前進させます。今回導出された数式は、破壊の精密な予測・制御の理論的基盤となり、従来の試行錯誤的なアプローチだけでなく、物理法則に基づく理論駆動型の材料設計を可能にします。亀裂先端の鋭化プロセスを制御することで、より強靭（きょうじん）で安全な材料の設計指針が得られます。

具体的には、自動車産業におけるタイヤや防振ゴムの耐久性向上、医療機器の安全性強化など、幅広い分野での応用が期待されます。材料の長寿命化は製品の交換頻度を減らし、廃棄物削減による環境負荷の低減にもつながります。本研究は、安全・安心な社会の構築と持続可能性の実現に貢献する、基礎科学からの重要な一歩です。

＜用語解説＞

注1）非線形効果

材料に加えた力と生じる変形が比例関係から外れることによる効果。通常、小さな変形の範囲では力を2倍にすると変形も2倍になる。しかし大きな変形では、この比例関係が成り立たなくなる。ゴム・ゲル・プラスチックなど、柔らかくよく伸びるポリマー材料では特に顕著に現れる。

注2）ポリマー材料（高分子材料）

小さい分子（モノマー）が多数つながり、ひも状や網状に結合した分子を高分子（ポリマー）という。高分子からなる材料がポリマー材料である。分子鎖の種類や結合様式により、プラスチック・ゴム・ゲル・繊維など多様な性質を示す。ゴムは長い分子鎖が化学的に架橋した網目構造を持ち、大きく伸びても元に戻る性質がある。ゲルは同様の網目構造に水などの液体を含んだもの。金属より軽量で成形しやすい利点があるが、薄くすると破れやすく、硬くするともろくなるのが課題であり、強靱なポリマー材料の開発が求められている。

注3）粘弾性

材料が示す弾性（バネ的な性質）と粘性（蜂蜜のようなネバネバした性質）を併せ持つ性質。ポリマー材料では、変形速度により応答が変化する。ゆっくり変形させると柔らかく振る舞い（ゴム状態）、速く変形させると硬くなる（ガラス状態）。中間の速度では粘性によるエネルギー散逸が起こる。この性質により、同じ材料でも亀裂の進展速度によって破壊の様相が劇的に変化する。力に比例して変形が生じる場合を線形弾性、力に比例して流れが生じる場合を線形粘性といい、両者を併せ持てば線形粘弾性という。今回は、線形粘弾性のみで亀裂先端の鋭化が生じることを示した。

注4）ド・ジェンヌ博士

フランスの理論物理学者（1932-2007）。1991年ノーベル物理学賞受賞。磁性体や超伝導体の研究で開発した理論手法を、高分子や液晶などのソフトマターに応用し、物理学の新分野を開拓した。スケーリング理論と呼ばれる手法で複雑な現象の本質を抽出し、「現代のニュートン」と称される。

注5）粘弾性トランペット理論

ド・ジェンヌ博士が1996年に提唱した、粘弾性材料の動的破壊を記述する理論。亀裂周辺を3つの領域に分け、各領域での変形がべき乗則（注8）に従うと予言。亀裂形状がトランペットのように広がることから命名。スケーリング理論とエネルギーバランスから導かれたが、連続体力学との関係は不明だった。本研究により初めて連続体力学の基礎方程式から導出され、30年越しに理論的正当性が証明された。

注6）連続体力学

物質を原子・分子の集合ではなく連続的な物体として扱い、その変形や流動を偏微分方程式で記述する理論体系。自動車・航空機や橋の安全設計から人工関節などの医療分野まで幅広く応用される。しかし粘弾性材料の動的破壊は方程式が複雑で解析が困難だった。本研究は新しい数学的手法（注7）により、この難問に初めて厳密解を与えた。

注7）新しい数学的手法

中学校の数学の図形では、適切な補助線を引くことで複雑な問題が簡単に解けることを習う。本研究でも似た発想の転換が鍵となった。ゴムの破壊では、材料全体が時々刻々と変形する複雑な動的問題を扱う。この変形は各点での「変位場」（電場や磁場のように空間の各点で定義されるベクトル量）で表される。本研究では、時間変化する複雑な変位場を、時間変化しない静的な変位場に変換する「補助場」を発見した。この補助場を用いて動的な亀裂進展を静止した亀裂の問題に変換し、比較的簡単な静止した亀裂の問題を解いてから元の動的な亀裂進展の問題に戻すという数学的工夫により、複雑な粘弾性材料の動的破壊に厳密解を与えた。

注8）べき乗則

物理量の間に「xのn乗に比例する」という関係が成り立つ法則。身近な例として、音の大きさは、音源から2倍離れると1/4に、3倍離れると1/9になる。これは、音源からの距離xの2乗に反比例する（x^-2に比例する）というべき乗則が成り立つためである。本研究では、亀裂先端からの距離xに対して、亀裂の開き幅が特定のべき乗（x^1/2、x^3/2）に従うことを発見した。x^1/2は丸い放物線形状、x^3/2はとがった形状を表し、べき乗則の指数nを特定することで亀裂形状の全体像を定量的に理解できる。